Bernoulli Equation Elevation Calculator

Velocity at Elevation 1 (\( V_1 \)):

Velocity at Elevation 2 (\( V_2 \)):

Height of Elevation 2 (\( h_2 \)):

Pressure at Elevation 1 (\( P_1 \)):

Pressure at Elevation 2 (\( P_2 \)):

Density of the Fluid (\( \rho \)):

Acceleration due to Gravity (\( g \)):

Elevation \( h_1 \) in meters (m):

Elevation \( h_1 \) in centimeters (cm):

Elevation \( h_1 \) in kilometers (km):

Elevation \( h_1 \) in yards (yard):

Elevation \( h_1 \) in feet (feet):

Elevation \( h_1 \) in miles (mile):

1. What is the Bernoulli Equation Elevation Calculator?

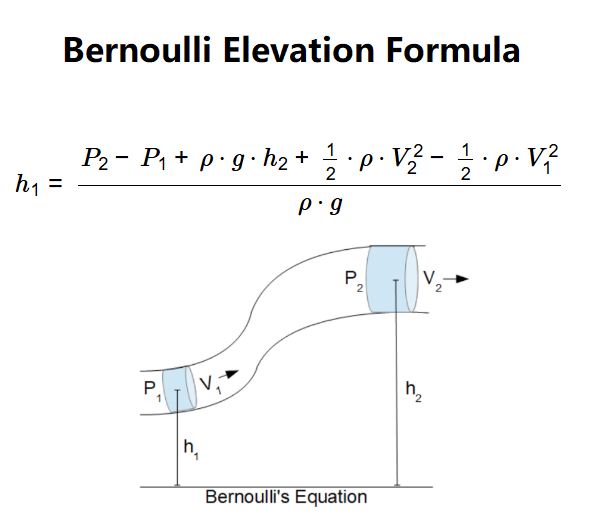
Definition: This calculator determines the elevation (\( h_1 \)) at point 1 using Bernoulli’s equation, based on velocities (\( V_1 \), \( V_2 \)), pressures (\( P_1 \), \( P_2 \)), elevation (\( h_2 \)), fluid density (\( \rho \)), and acceleration due to gravity (\( g \)).

Purpose: It assists engineers and physicists in analyzing fluid dynamics, particularly in systems involving elevation changes, such as pipelines or channels.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ h_1 = \frac{P_2 - P_1 + \rho \cdot g \cdot h_2 + \frac{1}{2} \cdot \rho \cdot V_2^2 - \frac{1}{2} \cdot \rho \cdot V_1^2}{\rho \cdot g} \]

Where:

\( h_1 \) — Elevation at point 1 (in various units)
\( V_1 \) — Velocity at elevation 1
\( V_2 \) — Velocity at elevation 2
\( h_2 \) — Elevation at point 2
\( P_1 \) — Pressure at elevation 1
\( P_2 \) — Pressure at elevation 2
\( \rho \) — Density of the fluid
\( g \) — Acceleration due to gravity

Explanation: Enter the velocities, pressures, elevation \( h_2 \), fluid density, and gravity in the chosen units, and the calculator computes the elevation \( h_1 \). Results use scientific notation (5 decimal places) if the elevation in meters is greater than 10000 or less than 0.00001, otherwise 2 decimal places. The image does not provide sample inputs or outputs beyond \( \rho = 998.2071 \, \text{kg/m}^3 \), so default values are used for testing.

3. Importance of Bernoulli’s Equation

Details: Bernoulli’s equation is fundamental in fluid dynamics, used to analyze the relationship between pressure, velocity, and elevation in a moving fluid, applicable in engineering fields like hydraulics and aerodynamics.

4. Using the Calculator

Tips: Enter positive values for velocities, pressures, elevation, and density, and ensure \( \rho \cdot g \neq 0 \), then click "Calculate." Results show the elevation \( h_1 \) in meters, centimeters, kilometers, yards, feet, and miles (scientific notation with 5 decimal places if > 10000 or < 0.00001 m, otherwise 2 decimal places).

Favorite