1. What is the Centripetal Force Calculator?

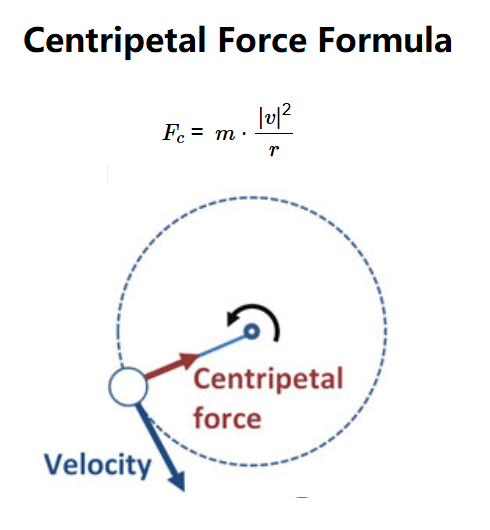
Definition: This calculator determines the centripetal force (\( F_c \)) required to keep an object in circular motion, based on its mass (\( m \)), tangential velocity (\( |v| \)), and radius (\( r \)).

Purpose: It assists in understanding the force directed toward the center of the circular path, useful in physics, engineering, and design applications such as orbital mechanics, vehicle dynamics, and amusement ride design.

2. How Does the Calculator Work?

The calculator uses the relationship:

Where:

• \( F_c \) — Centripetal force (in various units)
• \( m \) — Mass of the object
• \( |v| \) — Magnitude of the tangential velocity
• \( r \) — Radius of the circular motion

Explanation: Enter the radius, tangential velocity, and mass in the chosen units, and the calculator computes the centripetal force. Results use scientific notation (5 decimal places) if the force in newtons is greater than 10000 or less than 0.00001, otherwise 2 decimal places. For default inputs (\( r = 2 \, \text{m} \), \( |v| = 5 \, \text{m/s} \), \( m = 3 \, \text{kg} \)), the calculated force is 37.5 N.

3. Importance of Centripetal Force

Details: Centripetal force is the real force acting toward the center of the circular path, necessary to maintain circular motion. It’s crucial for analyzing dynamics in rotating systems, such as planetary orbits, centrifuges, and car cornering.

4. Using the Calculator

Tips: Enter positive values for radius, tangential velocity, and mass, and ensure \( r \neq 0 \), then click "Calculate." Results show the centripetal force in newtons, pound-force, dynes, and kilogram-force (scientific notation with 5 decimal places if > 10000 or < 0.00001 N, otherwise 2 decimal places).

Centripetal Force Calculator© - All Rights Reserved 2025