Continuity Equation (Velocity) Calculator

Area 1 (A₁):

Area 2 (A₂):

Velocity 2 (v₂):

Density 1 (ρ₁):

Density 2 (ρ₂):

Velocity 1 (m/s):

Velocity 1 (ft/s):

Velocity 1 (km/h):

Velocity 1 (mph):

1. What is the Continuity Equation for Velocity?

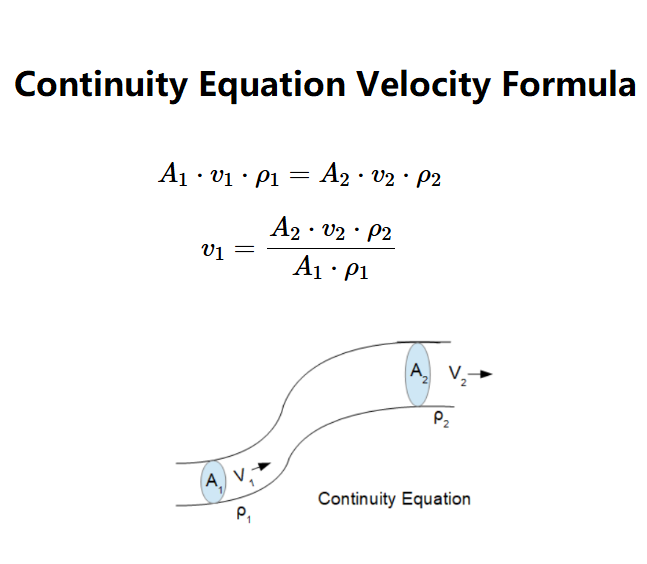
Definition: The continuity equation expresses the conservation of mass for a fluid flowing through a pipe or channel, allowing calculation of velocity at one section, using the formula:

\[ A_1 \cdot v_1 \cdot \rho_1 = A_2 \cdot v_2 \cdot \rho_2 \] \[ v_1 = \frac{A_2 \cdot v_2 \cdot \rho_2}{A_1 \cdot \rho_1} \]

Variables:

\( v_1 \): Velocity at section 1 (in m/s).
\( v_2 \): Velocity at section 2 (in m/s).
\( A_1 \): Cross-sectional area at section 1 (in m²).
\( A_2 \): Cross-sectional area at section 2 (in m²).
\( \rho_1 \): Density at section 1 (in kg/m³).
\( \rho_2 \): Density at section 2 (in kg/m³).

Explanation: This equation ensures that the mass flow rate remains constant between two sections of a flow, allowing the calculation of velocity when area and density change.

2. Importance of the Continuity Equation

Details: The continuity equation is fundamental in fluid dynamics to analyze and design systems involving fluid flow, such as pipes, ducts, and nozzles, ensuring mass conservation.

3. Using the Calculator

Tips: Enter the areas at sections 1 and 2, velocity at section 2, and densities at sections 1 and 2 with their respective units. Click "Calculate" to get the velocity at section 1 in multiple units.

Frequently Asked Questions (FAQ)

Q1: What is the continuity equation?
A: It is a mathematical statement of the conservation of mass for fluids, stating that the mass flow rate is constant through a system.

Q2: What does area represent in this context?
A: Area refers to the cross-sectional area of the flow path at different sections (e.g., pipes or ducts).

Q3: Why calculate velocity using the continuity equation?
A: It helps determine the velocity at one section of a flow when area or density changes, critical for fluid system design.

Q4: Can I use different units?
A: Yes, the calculator supports area units (m², cm², in², ft², yd²), velocity units (m/s, ft/s, km/h, mph), and density units (kg/m³, g/cm³, lb/ft³).

Q5: How accurate is this calculator?
A: The calculator is accurate based on the formula and input values, assuming steady flow. Real-world factors like turbulence may introduce variations.

Favorite