Critical Angle Calculator

Critical Angle (degrees):

Critical Angle (radians):

1. What is the Critical Angle?

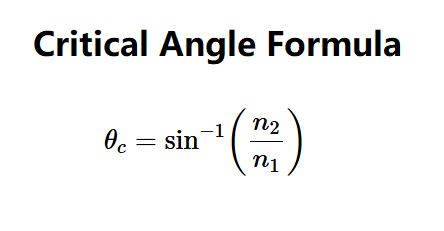
Definition: The critical angle is the angle of incidence at which the angle of refraction becomes 90 degrees, leading to total internal reflection, calculated using the formula:

\[ \theta_c = \sin^{-1} \left( \frac{n_2}{n_1} \right) \]

Variables:

\( \theta_c \): Critical angle (in degrees or radians).
\( n_1 \): Refractive index of medium 1 (denser medium, where the light is coming from, dimensionless).
\( n_2 \): Refractive index of medium 2 (less dense medium, where the light is entering, dimensionless).

Explanation: This formula applies when light travels from a denser medium (\( n_1 \)) to a less dense medium (\( n_2 \)), and the angle of incidence exceeds the critical angle, causing total internal reflection.

2. Importance of the Critical Angle

Details: The critical angle is fundamental in optics, particularly in applications like optical fibers, prisms, and endoscopes, where total internal reflection is used to guide light efficiently.

3. Using the Calculator

Tips: Enter the refractive indices of the two media. Ensure \( n_1 > n_2 \) (light must travel from a denser to a less dense medium). Click "Calculate" to get the critical angle in both degrees and radians.

Frequently Asked Questions (FAQ)

Q1: What is the critical angle?
A: The critical angle is the angle of incidence at which the angle of refraction is 90 degrees, leading to total internal reflection.

Q2: What is total internal reflection?
A: Total internal reflection occurs when light traveling from a denser to a less dense medium exceeds the critical angle, reflecting entirely within the denser medium.

Q3: What is the refractive index?
A: The refractive index (\( n \)) is a dimensionless number that describes how much light slows down and bends in a medium compared to a vacuum.

Q4: Why must \( n_1 \) be greater than \( n_2 \)?
A: Total internal reflection only occurs when light travels from a denser medium (\( n_1 \)) to a less dense medium (\( n_2 \)), ensuring \( \sin(\theta_c) \leq 1 \).

Q5: How accurate is this calculator?
A: The calculator is accurate based on Snell's Law and the input values, assuming ideal conditions. Real-world factors like dispersion or surface imperfections may introduce variations.

Favorite