Cylinder - Mass Moment of Inertia about z-axis

Mass (\( m \)):

Radius (\( R \)):

Height (\( h \)):

Mass Moment of Inertia (\( I_x = I_z \)) in kg·m²:

Mass Moment of Inertia (\( I_x = I_z \)) in g·cm²:

Mass Moment of Inertia (\( I_x = I_z \)) in lb·ft²:

Mass Moment of Inertia (\( I_x = I_z \)) in lb·in²:

1. What is the Mass Moment of Inertia Calculator?

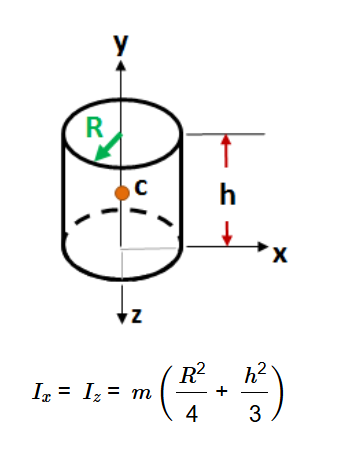
Definition: This calculator computes the mass moment of inertia (\( I_x = I_z \)) of a solid cylinder about the x or z axis (perpendicular to the cylinder's height), based on its mass (\( m \)), radius (\( R \)), and height (\( h \)).

Purpose: It is used in mechanics and engineering to analyze the resistance of a rotating cylinder to angular acceleration, applicable in designs involving rotating machinery, flywheels, and structural dynamics.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ I_x = I_z = m \left( \frac{R^2}{4} + \frac{h^2}{3} \right) \]

Where:

\( I_x = I_z \) — Mass moment of inertia about the x or z axis (in various units)
\( m \) — Mass of the cylinder
\( R \) — Radius of the cylinder's base
\( h \) — Height of the cylinder

Explanation: Enter the mass, radius, and height of the cylinder in the chosen units, and the calculator computes the mass moment of inertia. Results are displayed with 5 decimal places. For default inputs (\( m = 1 \, \text{kg} \), \( R = 0.1 \, \text{m} \), \( h = 0.5 \, \text{m} \)), the calculated mass moment of inertia \( I_x = I_z \) is approximately 0.09167 kg·m².

3. Importance of the Mass Moment of Inertia

Details: The mass moment of inertia quantifies an object's resistance to angular acceleration. It is essential for designing rotating systems, such as engines, turbines, and flywheels, to ensure stability and efficiency.

4. Using the Calculator

Tips: Enter positive values for mass, radius, and height with up to 4 decimal places (step of 0.0001), then click "Calculate." Results show the mass moment of inertia \( I_x = I_z \) in kg·m², g·cm², lb·ft², and lb·in², always with 5 decimal places.

Favorite