Force Magnitude (from components) Calculator

x-component of Force (\( F_x \)):

y-component of Force (\( F_y \)):

z-component of Force (\( F_z \)):

Force Magnitude (\( F \)) in Newtons (N):

Force Magnitude (\( F \)) in Pounds-Force (lbf):

Force Magnitude (\( F \)) in Dynes:

1. What is the Force Magnitude Calculator?

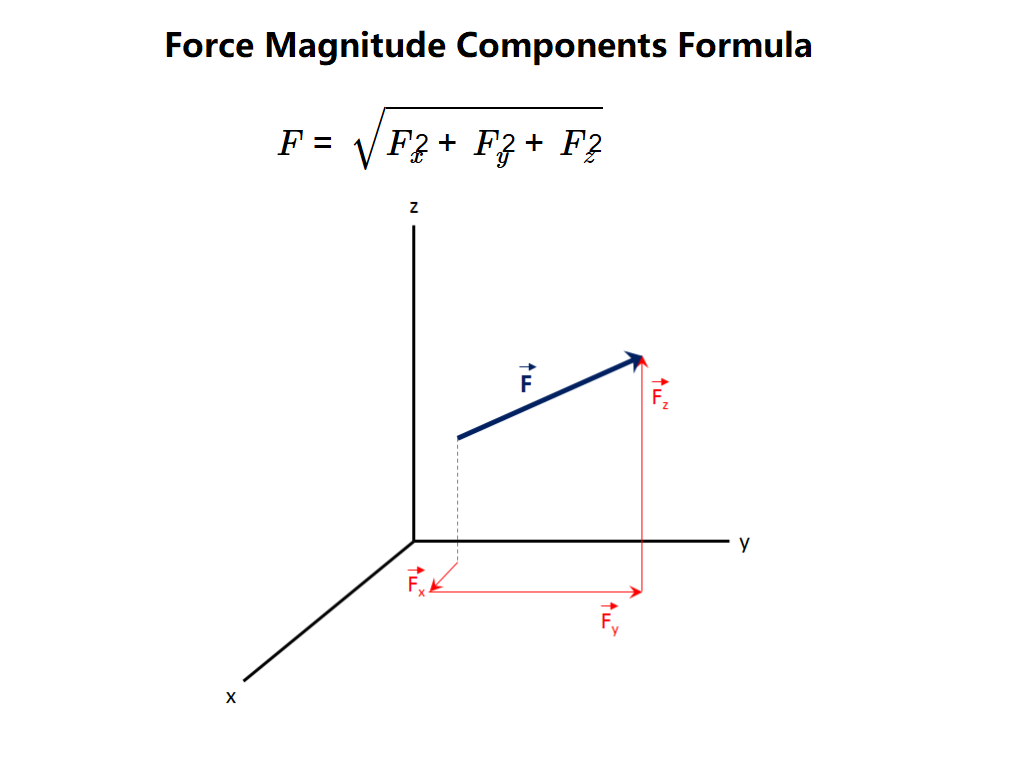
Definition: This calculator computes the magnitude of the force (\( F \)) based on its components in the x, y, and z directions (\( F_x \), \( F_y \), \( F_z \)) using the Pythagorean theorem.

Purpose: It is used in physics and engineering to determine the resultant force magnitude from its vector components, applicable in mechanics, structural analysis, and motion studies.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ F = \sqrt{F_x^2 + F_y^2 + F_z^2} \]

Where:

\( F \) — Magnitude of the force (in various units)
\( F_x \) — Force component in the x-direction
\( F_y \) — Force component in the y-direction
\( F_z \) — Force component in the z-direction

Explanation: Enter the components of the force in the x, y, and z directions in the chosen units, and the calculator computes the magnitude of the force. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( F_x = 2 \, \text{N} \), \( F_y = 3 \, \text{N} \), \( F_z = 4 \, \text{N} \)), the calculated force magnitude \( F \) is approximately 5.38516 Newtons.

3. Importance of Force Magnitude Calculation

Details: Calculating the magnitude of force from its components is crucial for analyzing the resultant effect of forces in three-dimensional systems, aiding in the design of structures, vehicles, and machinery.

FAQ

How do I find force magnitude?

Measure the force components in the x, y, and z directions in newtons. Compute the magnitude using the formula \( F = \sqrt{F_x^2 + F_y^2 + F_z^2} \). You will then have the force magnitude in Newtons.

How can I find a force component with magnitude and other components?

Measure the force magnitude in Newtons and the other two components in the same units. Use the equation \( F_x^2 + F_y^2 + F_z^2 = F^2 \) to solve for the unknown component, adjusting for the known values.

What is the formula for force magnitude?

The formula for the magnitude of a force vector is the square root of the sum of the squares of its components: \( F = \sqrt{F_x^2 + F_y^2 + F_z^2} \), where \( F_x \), \( F_y \), and \( F_z \) are the components in the x, y, and z directions, respectively. The standard unit is Newtons (N).

Favorite