Force from Mass and Change in Velocity over Time Calculator

Mass (\( M \)):

Change in Velocity (\( \Delta V \)):

Change in Time (\( \Delta T \)):

Force (\( F \)) in Newtons (N):

Force (\( F \)) in Pounds-Force (lbf):

Force (\( F \)) in Dynes:

1. What is the Force Calculator?

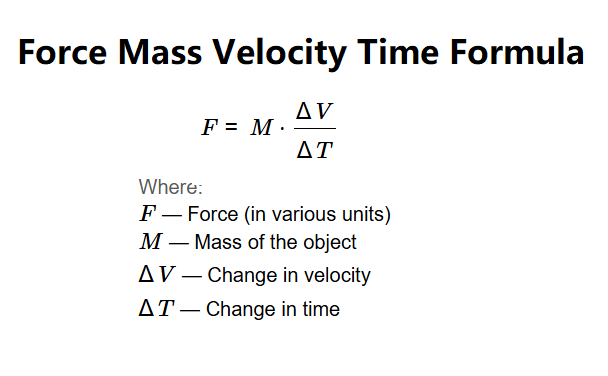
Definition: This calculator computes the force (\( F \)) acting on an object based on its mass (\( M \)), change in velocity (\( \Delta V \)), and change in time (\( \Delta T \)), using Newton's second law.

Purpose: It is used in physics and engineering to analyze the force exerted on objects undergoing a change in velocity over a period of time, applicable in mechanics, vehicle dynamics, and motion studies.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ F = M \cdot \frac{\Delta V}{\Delta T} \]

Where:

\( F \) — Force (in various units)
\( M \) — Mass of the object
\( \Delta V \) — Change in velocity
\( \Delta T \) — Change in time

Explanation: Enter the mass, change in velocity, and change in time in the chosen units, and the calculator computes the force. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( M = 1 \, \text{kg} \), \( \Delta V = 5 \, \text{m/s} \), \( \Delta T = 2.5 \, \text{s} \)), the calculated force \( F \) is 2.00000 Newtons.

3. Importance of Force Calculation

Details: Calculating force from mass and the rate of change of velocity is essential for understanding dynamics in physics, such as in collision analysis, propulsion systems, and motion control.

FAQ

How do I find force?

Measure the mass of the object in kilograms. Measure the change in velocity in meters/second and the change in time in seconds. Multiply the mass by the change in velocity divided by the change in time. You will then have the force in Newtons.

How can I find mass with force and acceleration?

Measure the force in Newtons. Measure the acceleration in meters/second². Divide the force by the acceleration. You will then have the mass of the object in kilograms.

What is the formula for force?

The formula for force is the mass of an object multiplied by its acceleration. In equation form, that's \( F = m \cdot a \), where \( F \) is the force, \( m \) is the mass, and \( a \) is the acceleration. The standard units are Newtons (N).

Favorite