Gravity Acceleration by Altitude Calculator

Gravitational Acceleration (\( g_h \)) in meters/second² (m/s²):

1. What is the Gravity Acceleration by Altitude Calculator?

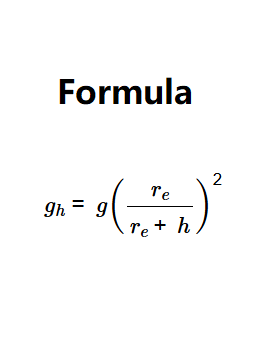
Definition: This calculator computes the gravitational acceleration (\( g_h \)) at a given altitude (\( h \)) above sea level based on the inverse-square law of gravitation.

Purpose: It is used in physics and engineering to determine the variation of gravitational acceleration with altitude, applicable in satellite orbits, atmospheric studies, and geophysical modeling.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ g_h = g \left( \frac{r_e}{r_e + h} \right)^2 \]

Where:

\( g_h \) — Gravitational acceleration at altitude (in m/s²)
\( g \) — Gravitational acceleration at sea level (\( 9.80665 \, \text{m/s}^2 \))
\( r_e \) — Earth's radius (\( 6,371,000 \, \text{m} \))
\( h \) — Altitude above sea level

Explanation: Enter the altitude above sea level in the chosen units, and the calculator computes the gravitational acceleration. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For the default input (\( h = 1000 \, \text{m} \)), the calculated gravitational acceleration \( g_h \) is approximately 9.80366 m/s².

3. Importance of Gravity Acceleration by Altitude

Details: Understanding how gravitational acceleration decreases with altitude is crucial for accurate calculations in aerospace, geophysics, and navigation systems, especially for objects at significant heights above the Earth's surface.

FAQ

How do I find gravitational acceleration at altitude?

Measure the altitude above sea level in meters. Use the formula \( g_h = g \left( \frac{r_e}{r_e + h} \right)^2 \), where \( g \) is 9.80665 m/s² and \( r_e \) is 6,371,000 m. You will then have the gravitational acceleration in m/s².

How can I find altitude with gravitational acceleration?

Measure the gravitational acceleration at a specific height in m/s². Use the relationship \( g_h = g \left( \frac{r_e}{r_e + h} \right)^2 \) and solve for \( h \) by rearranging: \( h = r_e \left( \frac{g}{g_h} \right)^{1/2} - r_e \), where \( g \) is 9.80665 m/s² and \( r_e \) is 6,371,000 m.

What is the formula for gravitational acceleration at altitude?

The formula for gravitational acceleration at altitude is \( g_h = g \left( \frac{r_e}{r_e + h} \right)^2 \), where \( g_h \) is the acceleration at altitude, \( g \) is the sea-level gravitational acceleration (9.80665 m/s²), \( r_e \) is the Earth's radius (6,371,000 m), and \( h \) is the altitude above sea level. The standard unit is m/s².

Favorite