Kinetic Energy of a Rigid Body Calculator

Mass (\( m \)):

Velocity (\( v \)):

Angular Velocity (\( \omega \)):

Mass Moment of Inertia (\( I_c \)):

Kinetic Energy (\( KE \)) in joules (J):

Kinetic Energy (\( KE \)) in kilojoules (kJ):

Kinetic Energy (\( KE \)) in foot-pounds (ft-lb):

1. What is the Kinetic Energy of a Rigid Body Calculator?

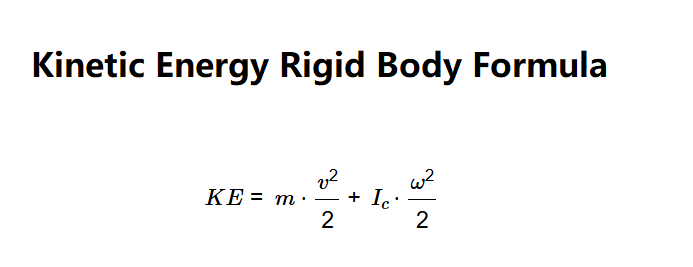
Definition: This calculator computes the total kinetic energy (\( KE \)) of a rigid body, accounting for both translational and rotational motion.

Purpose: It is used in classical mechanics to determine the energy associated with the linear and angular motion of a rigid body, applicable in engineering, robotics, and dynamics.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ KE = m \cdot \frac{v^2}{2} + I_c \cdot \frac{\omega^2}{2} \]

Where:

\( KE \) — Kinetic energy (in various units)
\( m \) — Mass
\( v \) — Linear velocity
\( I_c \) — Mass moment of inertia
\( \omega \) — Angular velocity

Explanation: Enter the mass, velocity, angular velocity, and mass moment of inertia in the chosen units, and the calculator computes the total kinetic energy. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( m = 2 \, \text{kg} \), \( v = 5 \, \text{m/s} \), \( \omega = 2 \, \text{rad/s} \), \( I_c = 1 \, \text{kg·m}^2 \)), the calculated kinetic energy \( KE \) is 27.00000 joules.

3. Importance of Kinetic Energy Calculation for a Rigid Body

Details: Calculating the kinetic energy of a rigid body is essential for analyzing the motion of rotating objects, aiding in the design of machinery, vehicles, and structures subjected to dynamic loads.

FAQ

How do I find the kinetic energy of a rigid body?

Measure the mass, linear velocity, angular velocity, and mass moment of inertia in your chosen units. Compute the kinetic energy using the formula \( KE = m \cdot \frac{v^2}{2} + I_c \cdot \frac{\omega^2}{2} \). The result will be in joules.

What is the difference between translational and rotational kinetic energy?

Translational kinetic energy (\( m \cdot \frac{v^2}{2} \)) depends on the linear motion of the center of mass, while rotational kinetic energy (\( I_c \cdot \frac{\omega^2}{2} \)) depends on the rotation about an axis through the center of mass.

What is the formula for the kinetic energy of a rigid body?

The formula for the kinetic energy of a rigid body is \( KE = m \cdot \frac{v^2}{2} + I_c \cdot \frac{\omega^2}{2} \), where \( m \) is the mass, \( v \) is the linear velocity, \( I_c \) is the mass moment of inertia, and \( \omega \) is the angular velocity. The standard unit for energy is joules (J).

Favorite