Mean Velocity Calculator

First Velocity (\( v_1 \)):

Duration at First Velocity (\( t_1 \)):

Second Velocity (\( v_2 \)):

Duration at Second Velocity (\( t_2 \)):

Mean Velocity (\( v_m \)) in meters/second (m/s):

Mean Velocity (\( v_m \)) in kilometers/hour (km/h):

Mean Velocity (\( v_m \)) in miles/hour (mph):

1. What is the Mean Velocity Calculator?

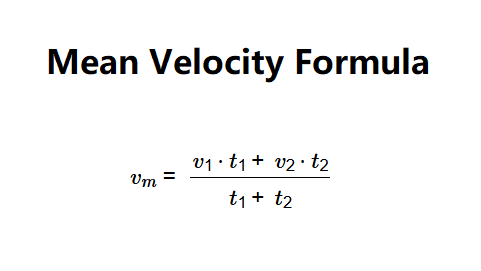
Definition: This calculator computes the mean velocity (\( v_m \)) of an object based on two different velocities (\( v_1 \), \( v_2 \)) and their respective durations (\( t_1 \), \( t_2 \)).

Purpose: It is used in physics to determine the average velocity over a journey with varying speeds, applicable in kinematics and motion analysis.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ v_m = \frac{v_1 \cdot t_1 + v_2 \cdot t_2}{t_1 + t_2} \]

Where:

\( v_m \) — Mean velocity (in various units)
\( v_1 \) — First velocity
\( t_1 \) — Duration at the first velocity
\( v_2 \) — Second velocity
\( t_2 \) — Duration at the second velocity

Explanation: Enter the first velocity, its duration, the second velocity, and its duration in the chosen units, and the calculator computes the mean velocity. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( v_1 = 10 \, \text{m/s} \), \( t_1 = 5 \, \text{s} \), \( v_2 = 20 \, \text{m/s} \), \( t_2 = 5 \, \text{s} \)), the calculated mean velocity \( v_m \) is 15.00000 m/s.

3. Importance of Mean Velocity Calculation

Details: Calculating mean velocity is essential for analyzing the overall motion of an object over time, aiding in understanding average speed in scenarios like vehicle travel, sports, and physics experiments.

FAQ

How do I find the mean velocity?

Measure the first velocity, its duration, the second velocity, and its duration in your chosen units. Compute the mean velocity using the formula \( v_m = \frac{v_1 \cdot t_1 + v_2 \cdot t_2}{t_1 + t_2} \). The result will be in meters/second.

What does mean velocity represent?

Mean velocity represents the average velocity of an object over a period of time, taking into account different velocities and their durations, providing a single value that reflects the overall motion.

What is the formula for mean velocity?

The formula for mean velocity is \( v_m = \frac{v_1 \cdot t_1 + v_2 \cdot t_2}{t_1 + t_2} \), where \( v_1 \) and \( v_2 \) are the velocities, and \( t_1 \) and \( t_2 \) are their respective durations. The standard unit for velocity is meters/second (m/s).

Favorite