Potential Energy of Gravity Calculator

Mass 1 (\( M_1 \)):

Mass 2 (\( m_2 \)):

Separation Distance (\( r \)):

Gravitational Potential Energy (\( U_g \)) in joules (J):

Gravitational Potential Energy (\( U_g \)) in kilojoules (kJ):

Gravitational Potential Energy (\( U_g \)) in megajoules (MJ):

1. What is the Potential Energy of Gravity Calculator?

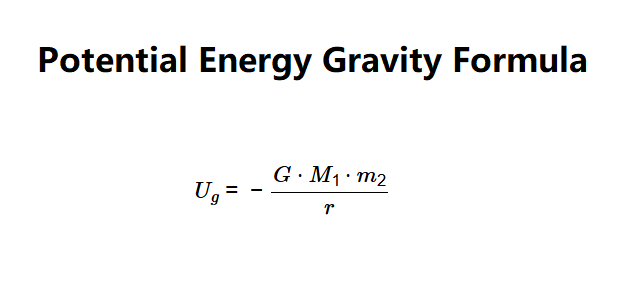
Definition: This calculator computes the gravitational potential energy (\( U_g \)) between two objects based on their masses (\( M_1 \), \( m_2 \)) and the separation distance (\( r \)).

Purpose: It is used in physics to determine the potential energy due to gravitational attraction, applicable in astrophysics, orbital mechanics, and gravitational studies.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ U_g = -\frac{G \cdot M_1 \cdot m_2}{r} \]

Where:

\( U_g \) — Gravitational potential energy (in various units)
\( G \) — Gravitational constant (\( 6.67430 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2} \))
\( M_1 \) — Mass of object 1
\( m_2 \) — Mass of object 2
\( r \) — Separation distance

Explanation: Enter the masses of the two objects and the separation distance in the chosen units, and the calculator computes the gravitational potential energy. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( M_1 = 1,000,000 \, \text{kg} \), \( m_2 = 1,000,000 \, \text{kg} \), \( r = 1 \, \text{km} \)), the calculated potential energy \( U_g \) is approximately \(-66.74300 \, \text{J}\).

3. Importance of Gravitational Potential Energy Calculation

Details: Calculating gravitational potential energy is crucial for understanding the energy associated with gravitational interactions, aiding in the study of planetary motion, satellite orbits, and other gravitational systems.

FAQ

How do I find the gravitational potential energy?

Measure the masses of the two objects in kilograms and the separation distance in meters. Compute the potential energy using the formula \( U_g = -\frac{G \cdot M_1 \cdot m_2}{r} \), where \( G = 6.67430 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2} \). The result will be in joules.

Why is gravitational potential energy negative?

Gravitational potential energy is negative because it represents the work needed to bring the objects from an infinite distance to their current separation, with the potential energy defined as zero at infinite separation.

What is the formula for gravitational potential energy?

The formula for gravitational potential energy is \( U_g = -\frac{G \cdot M_1 \cdot m_2}{r} \), where \( G \) is the gravitational constant, \( M_1 \) and \( m_2 \) are the masses, and \( r \) is the separation distance. The standard unit for energy is joules (J).

Favorite