Power for Vertical Lift Calculator

Mass of Object Lifted (\( m \)):

Height Lifted from Surface (\( h \)):

Time to Lift to Height (\( t \)):

Planetoid Object:

Power (\( P \)) in watts (W):

Power (\( P \)) in kilowatts (kW):

Power (\( P \)) in horsepower (hp):

Power (\( P \)) in BTU/hr:

1. What is the Power for Vertical Lift Calculator?

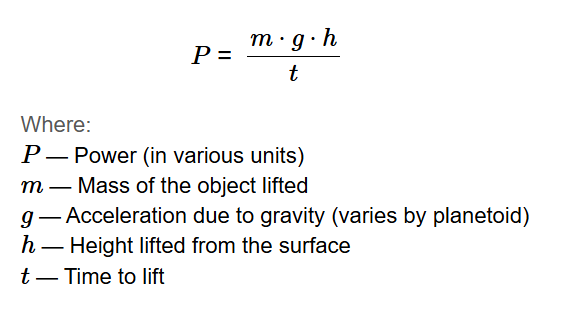
Definition: This calculator computes the power (\( P \)) required to lift an object vertically based on its mass (\( m \)), height (\( h \)), time (\( t \)), and the acceleration due to gravity (\( g \)) on a selected planetoid.

Purpose: It is used in physics and engineering to determine the power needed to perform vertical lift against gravity, applicable in space missions, aeronautics, and mechanical systems.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ P = \frac{m \cdot g \cdot h}{t} \]

Where:

\( P \) — Power (in various units)
\( m \) — Mass of the object lifted
\( g \) — Acceleration due to gravity (varies by planetoid)
\( h \) — Height lifted from the surface
\( t \) — Time to lift

Explanation: Enter the mass, height, time, and select the planetoid object to determine the acceleration due to gravity. The calculator computes the power. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( m = 10 \, \text{kg} \), \( h = 5 \, \text{m} \), \( t = 2 \, \text{s} \), planetoid = Earth (\( g = 9.81 \, \text{m/s}^2 \))), the calculated power \( P \) is approximately 245.25000 W.

3. Importance of Power for Vertical Lift Calculation

Details: Calculating power for vertical lift is essential for determining the energy requirements in lifting operations, aiding in the design of rockets, spacecraft, and other vertical lift systems across different planetary environments.

FAQ

How do I find the power required for vertical lift?

Measure the mass of the object in kilograms, the height in meters, the time in seconds, and select the planetoid to determine the acceleration due to gravity. Compute the power using the formula \( P = \frac{m \cdot g \cdot h}{t} \). The result will be in watts.

How does the planetoid affect the power calculation?

The planetoid determines the acceleration due to gravity (\( g \)), which varies across celestial bodies (e.g., 9.81 m/s² on Earth, 1.62 m/s² on the Moon). This affects the force required to lift the object, thus impacting the power.

What is the formula for power in vertical lift?

The formula for power in vertical lift is \( P = \frac{m \cdot g \cdot h}{t} \), where \( m \) is the mass, \( g \) is the acceleration due to gravity, \( h \) is the height, and \( t \) is the time. The standard unit for power is watts (W).

Favorite