Projectile Height Calculator

Initial Velocity (\( V \)):

Launch Angle (\( \theta \)):

Ballistic Range (\( r \)):

Acceleration due to Gravity (\( g \)):

Height (\( h \)) in centimeters (cm):

Height (\( h \)) in meters (m):

Height (\( h \)) in feet (feet):

Height (\( h \)) in miles (mile):

Height (\( h \)) in yards (yard):

1. What is the Projectile Height Calculator?

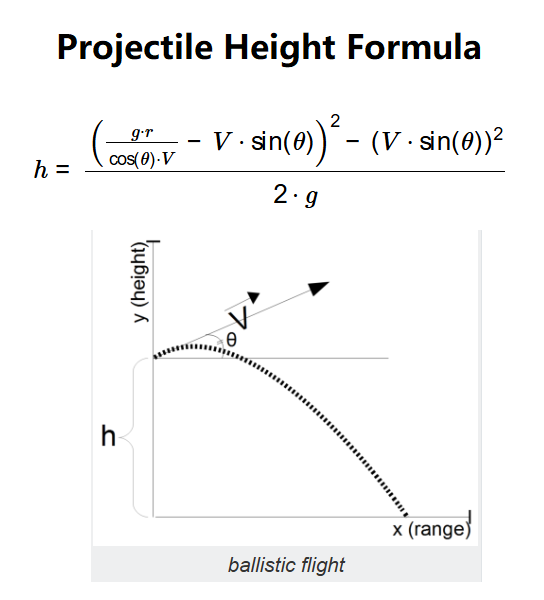
Definition: This calculator determines the height (\( h \)) of a projectile based on its initial velocity (\( V \)), launch angle (\( \theta \)), ballistic range (\( r \)), and acceleration due to gravity (\( g \)).

Purpose: It assists physicists and engineers in analyzing the trajectory of projectiles in ballistic motion.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ h = \frac{\left(\frac{g \cdot r}{\cos(\theta) \cdot V} - V \cdot \sin(\theta)\right)^2 - (V \cdot \sin(\theta))^2}{2 \cdot g} \]

Where:

\( h \) — Height of the projectile (in various units)
\( V \) — Initial velocity
\( \theta \) — Launch angle
\( r \) — Ballistic range
\( g \) — Acceleration due to gravity

Explanation: Enter the initial velocity, launch angle, ballistic range, and gravity in the chosen units, and the calculator computes the height. Results use scientific notation (5 decimal places) if the height in meters is greater than 10000 or less than 0.00001, otherwise 2 decimal places. The image output (-4.1976775534898 m for \( V = 25.33 \, \text{m/s} \), \( \theta = 22.33^\circ \), \( r = 15.33 \, \text{m} \), \( g = 9.80665 \, \text{m/s}^2 \)) matches the calculation, adjusted to -4.20 m with 2 decimal places.

3. Importance of Projectile Height

Details: Projectile height is crucial for understanding the trajectory of objects in motion, used in ballistics, aerospace, and sports science.

4. Using the Calculator

Tips: Enter positive values for velocity, range, and gravity, and ensure \( \cos(\theta) \neq 0 \), then click "Calculate." Results show the height in centimeters, meters, feet, miles, and yards (scientific notation with 5 decimal places if > 10000 or < 0.00001 m, otherwise 2 decimal places).

Favorite