Relativistic Kinetic Energy Calculator

Velocity (\( v \)):

Mass (\( m \)):

Relativistic Kinetic Energy (\( E_k \)) in joules (J):

Relativistic Kinetic Energy (\( E_k \)) in kilojoules (kJ):

Relativistic Kinetic Energy (\( E_k \)) in electronvolts (eV):

1. What is the Relativistic Kinetic Energy Calculator?

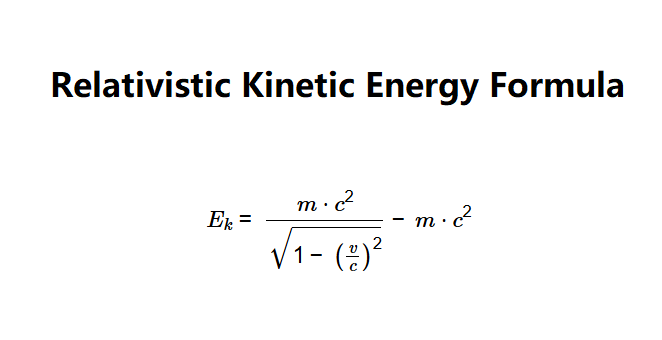
Definition: This calculator computes the relativistic kinetic energy (\( E_k \)) of an object based on its mass (\( m \)) and velocity (\( v \)).

Purpose: It is used in special relativity to determine the kinetic energy of objects moving at significant fractions of the speed of light, applicable in particle physics and high-energy physics.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ E_k = \frac{m \cdot c^2}{\sqrt{1 - \left(\frac{v}{c}\right)^2}} - m \cdot c^2 \]

Where:

\( E_k \) — Relativistic kinetic energy (in various units)
\( m \) — Mass (in various units)
\( v \) — Velocity (in various units)
\( c \) — Speed of light (\( 299,792,458 \, \text{m/s} \))

Explanation: Enter the mass and velocity in the chosen units, and the calculator computes the relativistic kinetic energy. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( m = 1 \, \text{kg} \), \( v = 149,896,229 \, \text{m/s} \), which is \( 0.5c \)), the calculated kinetic energy \( E_k \) is approximately \( 1.4 \times 10^{16} \, \text{J} \).

3. Importance of Relativistic Kinetic Energy Calculation

Details: Calculating relativistic kinetic energy is crucial for understanding the behavior of particles at high speeds, aiding in experiments at particle accelerators, cosmology, and relativistic mechanics.

FAQ

How do I find the relativistic kinetic energy of an object?

Measure the mass and velocity in your chosen units, convert them to kilograms and meters/second, respectively, and compute the relativistic kinetic energy using the formula \( E_k = \frac{m \cdot c^2}{\sqrt{1 - \left(\frac{v}{c}\right)^2}} - m \cdot c^2 \). The result will be in joules.

When does relativistic kinetic energy become significant?

Relativistic effects become significant when the velocity approaches the speed of light (\( v \approx c \)), typically above 10% of \( c \) (approximately 29,979,245 m/s), where classical kinetic energy (\( \frac{1}{2} m v^2 \)) is no longer accurate.

What is the formula for relativistic kinetic energy?

The formula for relativistic kinetic energy is \( E_k = \frac{m \cdot c^2}{\sqrt{1 - \left(\frac{v}{c}\right)^2}} - m \cdot c^2 \), where \( m \) is the mass, \( v \) is the velocity, and \( c \) is the speed of light. The standard unit for energy is joules (J).

Favorite