Terminal Velocity Calculator by Area

Surface Area (\( A \)):

Drag Coefficient (\( C_d \)) (0 to 1):

Air Density (\( \rho \)):

Planetoid Object (for \( g \)):

Mass (\( m \)):

Terminal Velocity (\( v_t \)) in meters/second (m/s):

Terminal Velocity (\( v_t \)) in kilometers/hour (km/h):

Terminal Velocity (\( v_t \)) in miles/hour (mph):

1. What is the Terminal Velocity Calculator?

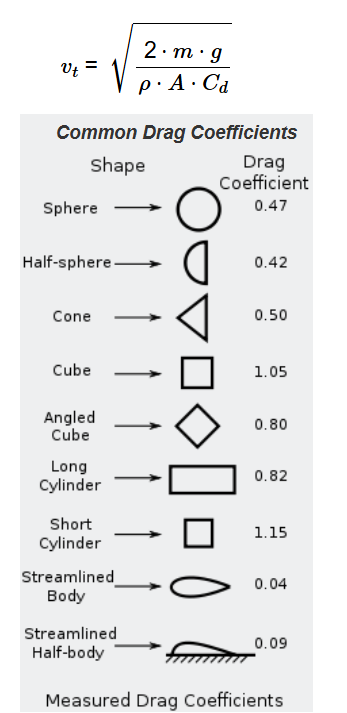
Definition: This calculator computes the terminal velocity (\( v_t \)) of a falling object based on its mass (\( m \)), gravitational acceleration (\( g \)), air density (\( \rho \)), surface area (\( A \)), and drag coefficient (\( C_d \)).

Purpose: It is used in physics to determine the constant velocity an object reaches when the gravitational force is balanced by the drag force, applicable in studies of aerodynamics, skydiving, and fluid dynamics.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ v_t = \sqrt{\frac{2 \cdot m \cdot g}{\rho \cdot A \cdot C_d}} \]

Where:

\( v_t \) — Terminal velocity (in various units)
\( m \) — Mass of the falling object
\( g \) — Gravitational acceleration (varies by planetoid)
\( \rho \) — Air density
\( A \) — Surface area of the object in the direction of motion
\( C_d \) — Drag coefficient (0 to 1)

Explanation: Enter the surface area, drag coefficient, air density, select the planetoid to determine gravitational acceleration, and enter the mass in the chosen units. The calculator computes the terminal velocity. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( A = 0.1 \, \text{m}^2 \), \( C_d = 0.5 \), \( \rho = 1.2754 \, \text{kg/m}^3 \), planetoid = Earth (\( g = 9.81 \, \text{m/s}^2 \)), \( m = 1 \, \text{kg} \)), the calculated terminal velocity \( v_t \) is approximately 17.52066 m/s.

3. Importance of Terminal Velocity Calculation

Details: Calculating terminal velocity is essential for understanding the maximum speed an object can reach while falling through a fluid, aiding in the design of parachutes, aircraft, and other systems involving drag forces.

FAQ

How do I find the terminal velocity of a falling object?

Measure the mass in kilograms, surface area in square meters, air density in kg/m³, select the planetoid to determine gravitational acceleration, and specify the drag coefficient. Compute the terminal velocity using the formula \( v_t = \sqrt{\frac{2 \cdot m \cdot g}{\rho \cdot A \cdot C_d}} \). The result will be in meters/second.

What does terminal velocity represent?

Terminal velocity represents the constant speed an object reaches when the gravitational force is balanced by the drag force, meaning the object no longer accelerates and falls at a steady rate.

What is the formula for terminal velocity?

The formula for terminal velocity is \( v_t = \sqrt{\frac{2 \cdot m \cdot g}{\rho \cdot A \cdot C_d}} \), where \( m \) is the mass, \( g \) is the gravitational acceleration, \( \rho \) is the air density, \( A \) is the surface area, and \( C_d \) is the drag coefficient. The standard unit for velocity is meters/second (m/s).

Favorite