Undamped Natural Circular Frequency Calculator

Static Deflection (\( \delta_{st} \)):

Planetoid Object (for \( g \)):

Undamped Natural Circular Frequency (\( \omega_n \)) in radians/second (rad/s):

Undamped Natural Circular Frequency (\( \omega_n \)) in degrees/second (deg/s):

Undamped Natural Circular Frequency (\( \omega_n \)) in revolutions/second (rev/s):

1. What is the Undamped Natural Circular Frequency Calculator?

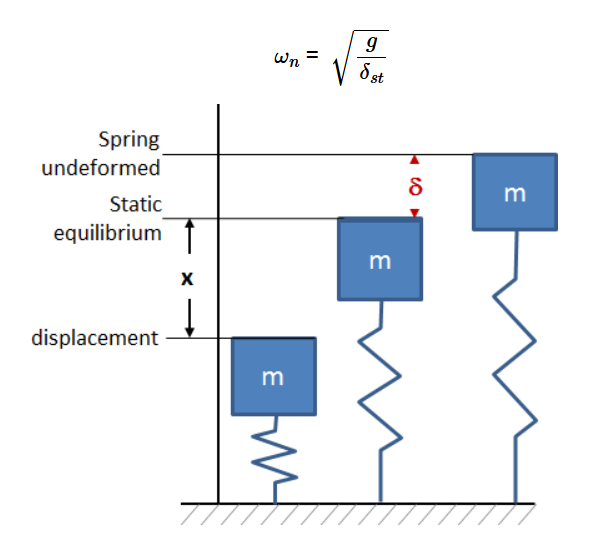
Definition: This calculator computes the undamped natural circular frequency (\( \omega_n \)) of a system based on the acceleration due to gravity (\( g \)) and the static deflection (\( \delta_{st} \)).

Purpose: It is used in physics and engineering to determine the natural frequency of an undamped oscillatory system, applicable in studies of vibrations, springs, and pendulums.

2. How Does the Calculator Work?

The calculator uses the relationship:

\[ \omega_n = \sqrt{\frac{g}{\delta_{st}}} \]

Where:

\( \omega_n \) — Undamped natural circular frequency (in various units)
\( g \) — Acceleration due to gravity (varies by planetoid)
\( \delta_{st} \) — Static deflection

Explanation: Enter the static deflection and select the planetoid to determine the acceleration due to gravity. The calculator computes the undamped natural circular frequency. Results are displayed with 5 decimal places, using scientific notation if the value exceeds 100,000 or is less than 0.0001. For default inputs (\( \delta_{st} = 0.01 \, \text{m} \), planetoid = Earth (\( g = 9.81 \, \text{m/s}^2 \))), the calculated frequency \( \omega_n \) is approximately 31.32092 rad/s.

3. Importance of Undamped Natural Circular Frequency Calculation

Details: Calculating the undamped natural circular frequency is essential for understanding the oscillatory behavior of systems without damping, aiding in the design of mechanical systems, vibration control, and structural analysis.

FAQ

How do I find the undamped natural circular frequency?

Measure the static deflection in meters and select the planetoid to determine the acceleration due to gravity. Compute the frequency using the formula \( \omega_n = \sqrt{\frac{g}{\delta_{st}}} \). The result will be in radians/second.

What does undamped natural circular frequency represent?

Undamped natural circular frequency represents the frequency at which a system oscillates without damping, determined by the system’s stiffness and mass distribution.

What is the formula for undamped natural circular frequency?

The formula for undamped natural circular frequency is \( \omega_n = \sqrt{\frac{g}{\delta_{st}}} \), where \( g \) is the acceleration due to gravity, and \( \delta_{st} \) is the static deflection. The standard unit for frequency is radians/second (rad/s).

Favorite